Convertir hexadecimal, binario y decimal

Vamos a ver cómo hacer conversiones entre los sistemas hexadecimal, binario y decimal.

En este artículo:

2. El Sistema HEXADECIMAL
- 2.1 Ejemplo Conversion de Hexadecimal a Decimal
  - 2.1. a) Ejercicio : Pasar de hexadecimal a decimal

2.2 Ejemplo CONVERSIÓN Decimal a Hexadecimal
- 2.2 a) Ejercicio : Pasar de decimal a hexadecimal

2.3 CALCULADORA Hexadecimal a Decimal y viceversa

3. El ¿Cómo funciona el Sistema Binario?
- 3.1 Ejemplo convertir numero decimal a binario
  - 3.1 a) Ejercicio : Pasar de decimal a binario

- 3.2 CALCULADORA Binario a Decimal y viceversa

1. Vamos a ver una tabla de conversión decimal, hexadecimal y binario.

**TABLA DE CONVERSIÓN DECIMAL, HEXADECIMAL (base 16) y BINARIO (base 2)**
0	0	0000
NÚMERO DECIMAL	NÚMERO HEXADECIMAL	NÚMERO BINARIO
1	1	0001
2	2	0010
3	3	0011
4	4	0100
5	5	0101
6	6	0110
7	7	0111
8	8	1000
9	9	1001
10	A	1010
11	B	1011
12	C	1100
13	D	1101
14	E	1110
15	F	1111

Otros números útiles convertidos en Hexadecimal binario:

**Otras conversiones Hexadecimal-binario-decimal**
25	19	11001
NÚMERO DECIMAL	NÚMERO HEXADECIMAL	NÚMERO BINARIO
50	32	110010
100	64	1100100
200	c8	11001000
300	12c	100101100
400	190	110010000
500	1f4	111110100
1000	3e8	1111101000

2. ¿Qué es, para qué sirve y cómo funciona el sistema HEXADECIMAL?

Los números hexadecimales se basan en potencias de 16, y se representan con 0x delante.
El sistema hexadecimal se utiliza en la informática y computación, junto con el sistema binario. Una de las utilidades que tiene es representar direcciones de memoria.

El sistema hexadecimal también se utiliza para representar colores en el diseño web. Los dos primeros dígitos representan el color rojo, los dos siguientes el verde, y los dos últimos el azul. Por ejemplo, #000000 es negro, mientras que #FFFFFF es blanco.

Otros colores más complejos se crean utilizando los tres colores, por ejemplo, el color #1C3ED1, que es un azul oscuro como este:

2.1 Convertir numero hexadecimal a decimal (pasar de base 10 a base 16)

¿Cuál es el decimal del número hexadecimal AE ?

Tenemos el número Hexadecimal AE, o 0xAE (los hexadecimales se identifican con un 0x delante. )

Para convertir hexadecimal a decimal, antes tenemos que convertir el número hexadecimal en binario:
A (hexadecimal) es 1010 (binario)
E (hexadecimal) es 1110 (binario)

–> Así que en binario sería 10101110

Convirtiéndolo a decimal (damos valor a las potencias de 2 en su posición) :
2^7 + 0 + 2^5 + 0 + 2^3 + 2^2 + 2^1 + 0 = 174

Resultado: el número Hexadecimal AE es igual a 174 en decimal.

2.1. a) Ejercicio : Pasar de hexadecimal a decimal

2.2 ¿Cómo convertir numero decimal a hexadecimal?

Para convertir un número decimal a hexadecimal, primero convertiremos el decimal a binario, dividiendo el número 174 entre 2, todas las veces necesarias, hasta llegar al final de las divisiones posibles.

(Posteriormente, convertiremos fácilmente el número binario a hexadecimal).

Al final recogemos el último cociente, y añadimos todos los restos de las divisiones, de derecha a izquierda, de esta forma:

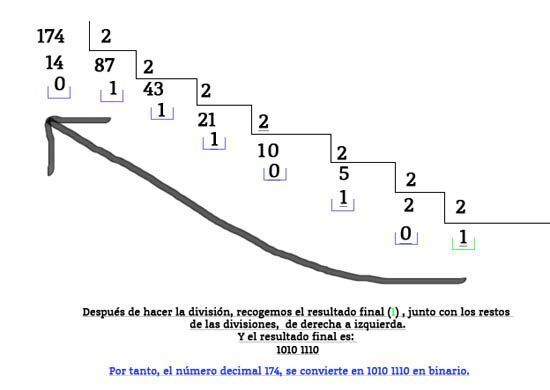
Resultado: el número decimal 174 es igual a 1010 1110 en binario.

Y después usaremos la Tabla de conversiones de sistemas numericos: conversión hexadecimal, decimal y binario, y veremos que convertimos ese binario en hexadecimal, y el resultado será AE, o como decíamos antes 0xAE

2.2 a) Ejercicio : Pasar de decimal a hexadecimal

2.3 CALCULADORA para convertir de Hexadecimal a decimal y viceversa

(Autoría: CalcuWorld)

3.¿Cómo funciona el Sistema Binario?

El sistema de número binarios se basa en las potencias de 2. Se usa enormemente en el direccionamiento IP y la construcción de redes, teniendo en cuenta el número de hosts.

El modo o sistema binario utiliza bits para transmitir información, según haya información (bit en valor 1 = hay info) o no haya información (bit en valor 0 = no hay info). Es muy común utilizar el modo binario para ciertas operaciones informáticas o matemáticas, y posteriormente realizar conversiones a otros sistemas, como por ejemplo el decimal, el hexadecimal y el octal.

3.1 Ejemplo CONVERSIÓN Decimal a Binario

Para realizar la conversión a binario, dividimos el número decimal (en este ejemplo es el 174) entre 2, todas las veces necesarias, hasta llegar al final de las divisiones posibles, y recogiendo cada vez el resultado de la división.